Numeri: Ambi: Terni: Quaterne: Cinquine: Sestine: Settine: 1—–2: 1—–3: 3: 1—–4: 6: 4: 1—–5: 10: 10: 5: 1—–6: 15: 20: 15: 6: 1—7: 21: 35: 35: 21: 7: 1: 8: 28: 56: 70: 56: 28: 8: 9: 36: 84: 126: 126: 84: 36: 10: 45: 120: 210: 252: 210: 120. k è la quantità di numeri della combinazione. Per “k!” s’intende il fattoriale che è calcolato come : k!=k* (k-1)* (k-2)*..*k*1. Ad esempio il fattoriale di 5 è 5*4*3*2*1=120. Nel caso si voglia conoscere le combinazioni che compongono una cinquina avremo: 5*4/2=10 Ambi. (5*4*3)/ (3*2)=10 Terni. (5*4*3*2)/ (4*3*2)=5 Quaterne.
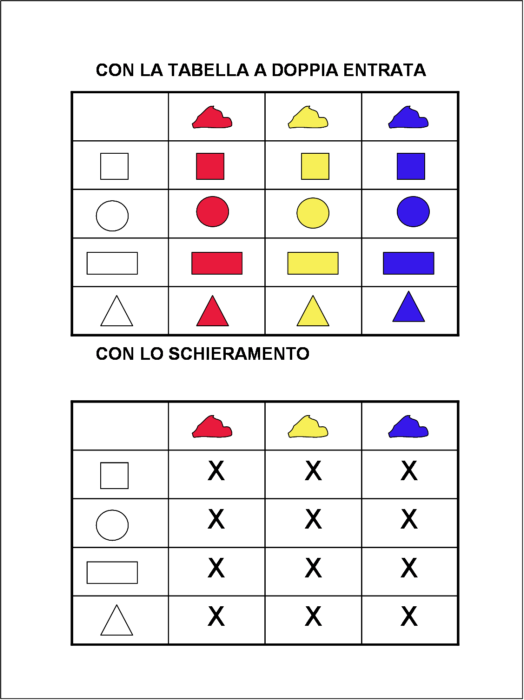
didattica matematica scuola primaria gennaio 2016

Combinazioni semplici e con ripetizione. Matematica quarta superiore

Scuola di Ballo “STELLE NASCENTI” Free Printable Bingo Cards, Chinese New Year Crafts, New Year

NUMERO 5 matematica classe 1^ MaestraMonica

il vento è forte fattibile Avere a che fare con come calcolare le combinazioni di numeri Palude

Diario di una ragazza indaco Numeri doppi Combinazioni con lo Zero

il vento è forte fattibile Avere a che fare con come calcolare le combinazioni di numeri Palude

Combinazioni con ripetizione 1 YouTube

Quante combinazioni puoi fare con i numeri 1,2,3? GufoSaggio
Pensieri in libertà Come calcolare le combinazioni del lotto con EXCEL

Calcolo combinatorio Excel funzione COMBINAZIONE Excel per tutti

Combinazioni semplici e con ripetizione Spiegazione ed esempi YouTube

PRIMA DECINAnumero 10matematica classe 2^ MaestraMonica

Sistemi Di Due Equazioni In Due Incognite cardays

Schede didattiche di matematica moltiplicare per 10, 100, 1000 Fantavolando Matematica

Esercizi sui Numeri Primi per la Scuola Primaria Schede di matematica, Matematica, Lezioni di

Quante Combinazioni Con 6 Numeri Da 0 A 9?
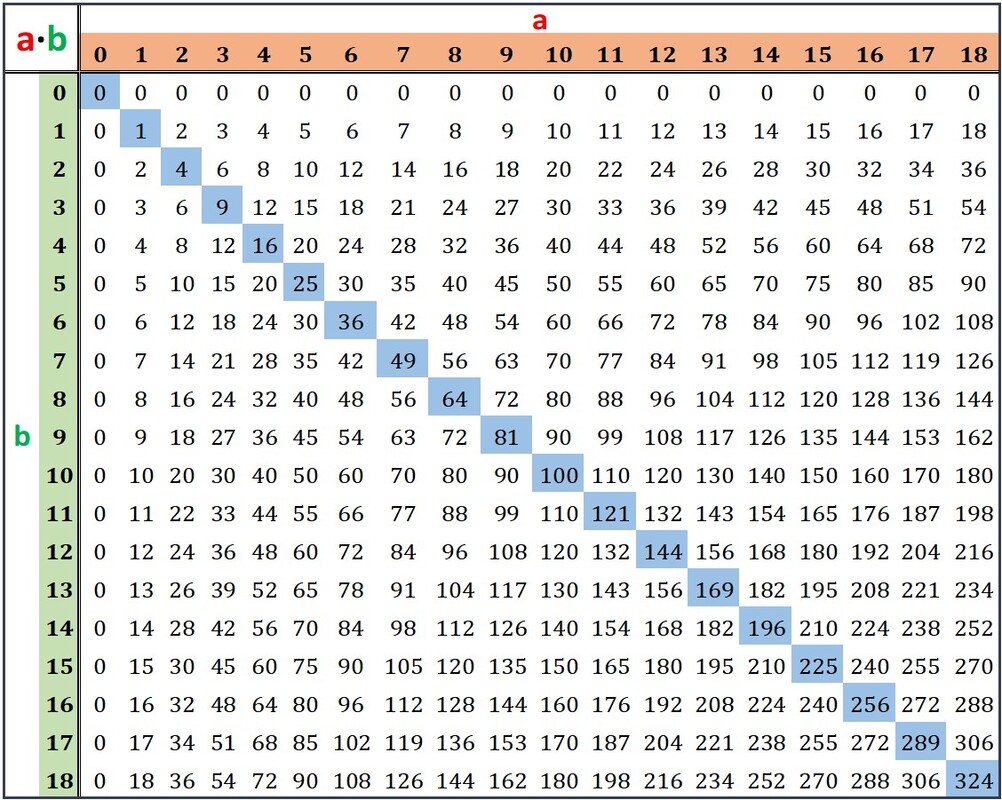
Tabellina per moltiplicazioni €3.33 mackworld.lk

Lezioni Settimana 2

Combinazioni semplici, esercizi svolti YouTube
Si dice combinazione semplice ogni sequenza di k elementi distinti estratti tra n elementi distinti, indipendentemente dall’ordine e con n ≥ k. Il numero di combinazioni semplici si indica con C_ (n,k) ed è dato dal coefficiente binomiale n su k. C_ (n,k) = binom (n) (k) = (n!)/ (k! (n−k)!) Combinazioni con ripetizione.. C (4,2)=\frac {4!} {2! (4-2)!}=\frac {4!} {2!2!}=\frac {4 × 3 × 2 × 1} { (2 × 1) (2 × 1)}=\frac {24} {4}=6 C (4,2) = 2!(4− 2)!4! = 2!2!4! = (2×1)(2× 1)4× 3× 2×1 = 424 = 6. Questo è esattamente ciò che il Calcolatore di Combinazioni calcola. Esempio 2.


