Una generalizzazione del teorema di Pitagora è il teorema del coseno, che si applica ad un triangolo qualsiasi (non necessariamente retto).In un triangolo con vertici e angoli indicati come in figura, vale l’uguaglianza: ¯ = ¯ + ¯ ¯ ¯ . Nel caso in cui sia retto, vale = e quindi l’enunciato è equivalente al teorema di Pitagora. Il termine aggiuntivo può essere interpretato come.. In geometria il Teorema di Pitagora è, probabilmente, il teorema più conosciuto. Il Teorema di Pitagora si applica ai triangoli rettangoli, ma esistono molteplici applicazioni anche nelle altre figure piane e nei solidi. Innanzitutto vediamo cosa prevede questo teorema: il quadrato costruito sull’ipotenusa è equivalente alla somma dei.

MATEMATICA, SCIENZE, EDUCAZIONE Teorema di Pitagora ed applicazioni
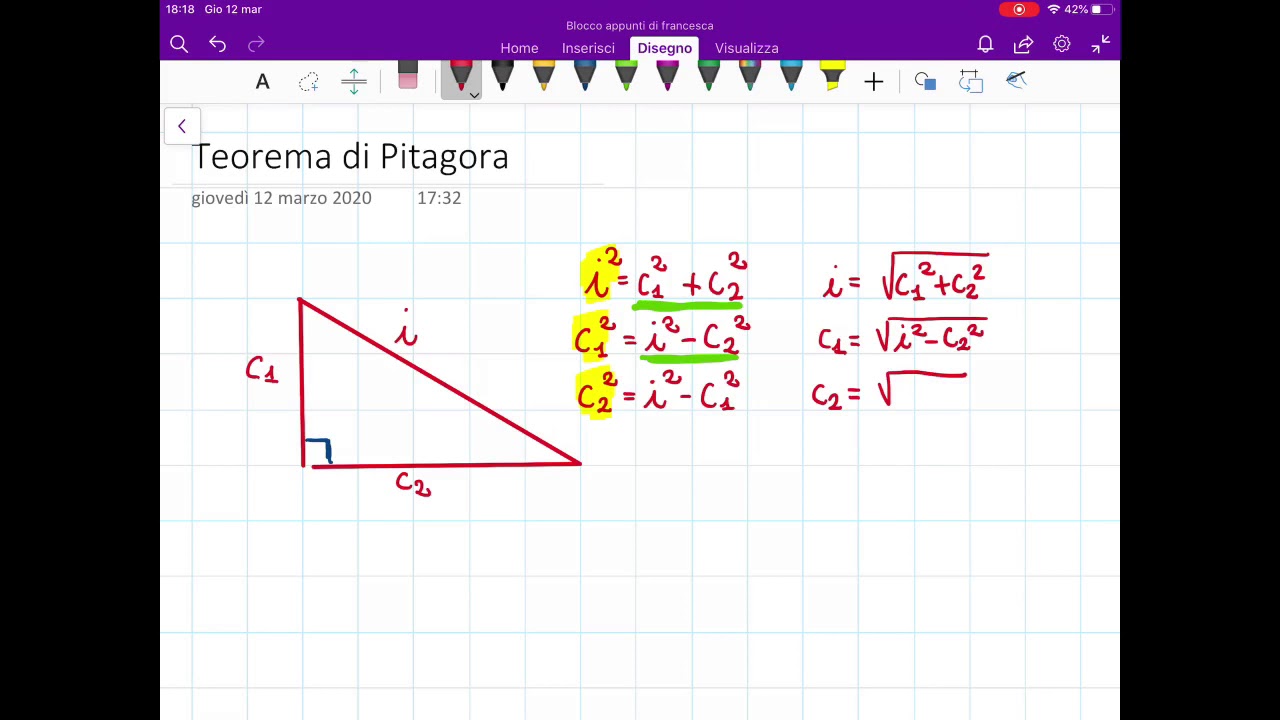
Il Teorema Di Pitagora Introduzione YouTube
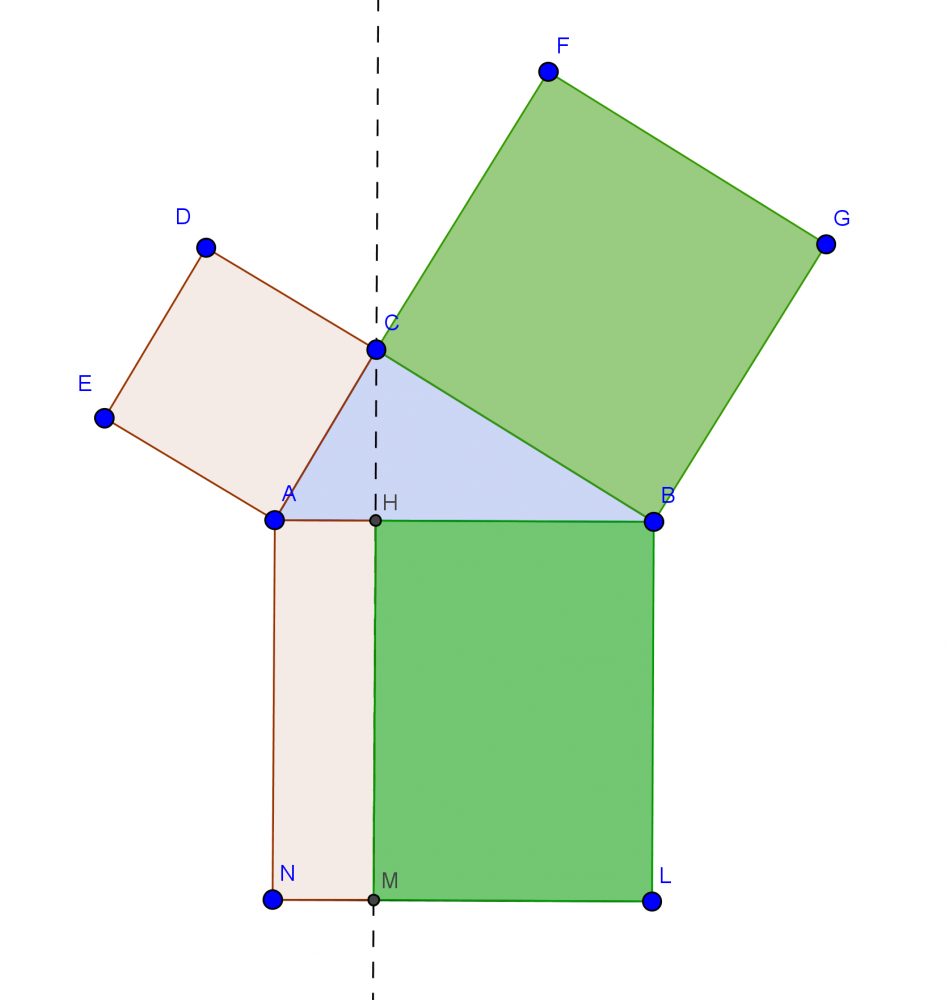
Il Teorema di Pitagora

Teorema di Pitagora Studentville

PPT TEOREMA DI PITAGORA PowerPoint Presentation, free download ID3050135
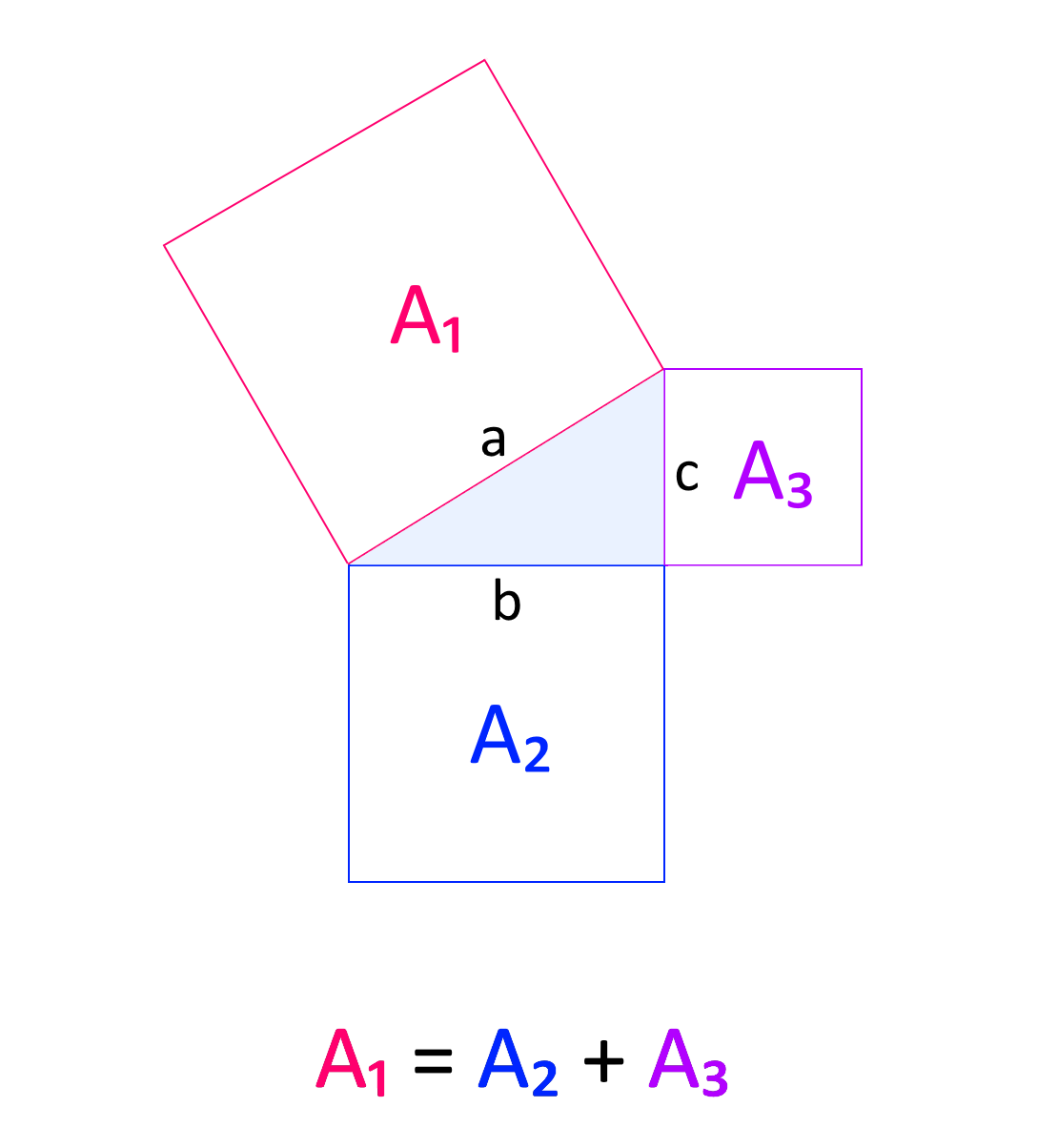
Teorema di Pitagora (con semplice dimostrazione ed esempi) Altramatica

Il teorema di Pitagora nei triangoli con angoli di 45°. Matematica seconda media

9 dimostrazioni del teorema di Pitagora YouTube

Applicazioni del Teorema di Pitagora YouTube

Il Teorema di Pitagora YouTube

Il teorema di Pitagora YouTube

Teorema di Pitagora Esempio 4 Problema su Rombo YouTube
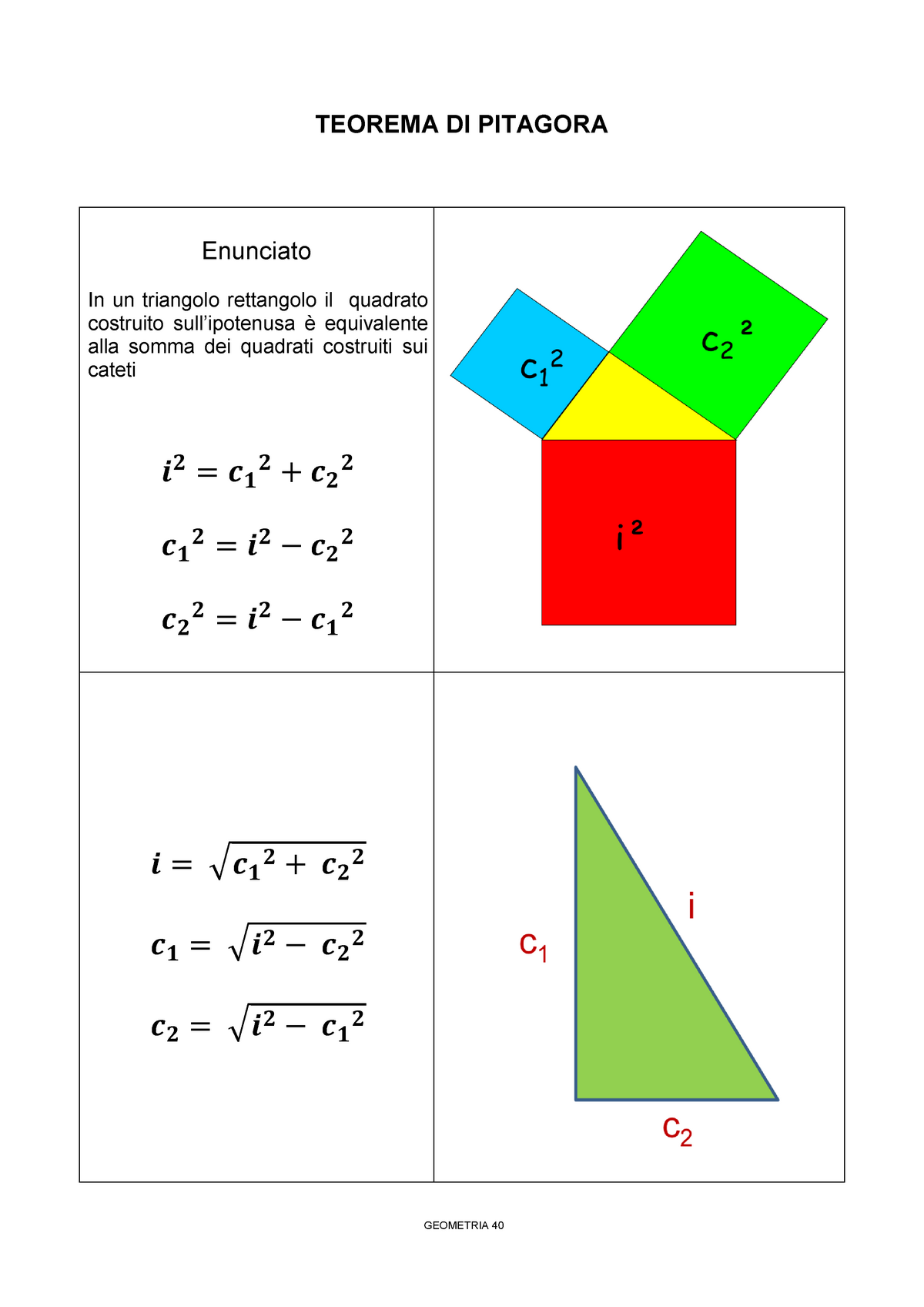
Teorema di Pitagora appunti lezioni fisica con elementi di matematica TEOREMA DI PITAGORA

Il Teorema di Pitagora come non l’hai mai visto YouTube

Problemi Teorema di Pitagora Mauitaui e la matematica

Il teorema di Pitagora applicato al rombo Matematica Facile Teorema di pitagora, Fogli di

Teorema di Pitagora Lettera43

Terne pitagoriche e inverso del teorema di Pitagora per Medie Redooc

Problemi con il Teorema di Pitagora YouTube

Applicazioni del Teorema di Pitagora YouTube
In qualsiasi triangolo rettangolo, i lati che toccano l’angolo retto sono i cateti. Invece il lato opposto all’angolo retto è l’ipotenusa. Continuiamo con il Teorema di Pitagora applicato al parellelogramma. Nel nostro esempio conosciamo la lunghezza dell’ipotenusa e di uno dei cateti. Per calcolare la lunghezza dell’altro cateto.. Ci sono vari enunciati per il teorema di Pitagora, così come varie sono le sue applicazioni.. e sui cateti (c1^2, c2^2) si ottiene elevando al quadrato il dato relativo, per cui avremo: $$ i^2 = c1^2 + c2^2 $$ Una volta compresa questa relazione tra i dati è possibile ricavare velocemente anche le formule inverse del teorema di Pitagora.


